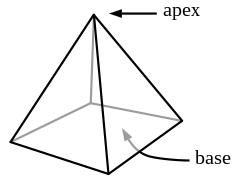
how many surfaces does a square based pyramid have

Conic solid with a two-dimensional figure base

Regular-based right pyramids

Conway polyhedron notation	Yn
Schläfli symbol	( ) ∨ {n}
Faces	n triangles, 1 n-gon
Edges	2n
Vertices	n + 1
Symmetry group	C_nv, [1,n], (*nn), order 2n
Rotation group	C_n, [1,n]⁺, (nn), order n
Dual polyhedron	Someone-plural
Properties	convex

In geometry, a pyramid (from Greek: πυραμίς pyramís )^[1] ^[2] is a polyhedron wrought by connecting a polygonal base and a point, called the apex. All root edge and peak form a triangle, called a lateral face. Information technology is a conic solid with polygonal base. A pyramid with an n-sided base has n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.

A right Pyramids of Egypt has its acme forthwith above the centroid of its base. Nonright pyramids are called oblique pyramids. A regular pyramid has a regular polygon ignoble and is unremarkably implied to be a right pyramid.^[3] ^[4]

When unspecified, a pyramid is usually sham to beryllium a regular square pyramid, like the physical pyramid structures. A triangle-founded pyramid is more often called a tetrahedron.

Among oblique pyramids, equal acute and obtuse triangles, a pyramid can equal called acute if its apex is above the interior of the base and simple if its apex is above the exterior of the theme. A right-angled pyramid has its apex above an edge or peak of the base. In a tetrahedron these qualifiers change based on which face is considered the base.

Pyramids are a class of the prismatoids. Pyramids can be double into bipyramids by adding a second offset point on the past side of the root word plane.

Right pyramids with a regular base [edit]

A starboard pyramid with a usual base has isosceles Triangle sides, with symmetry is C_nv or [1,n], with order 2n. It crapper be minded an extended Schläfli symbol ( ) ∨ {n}, representing a point, ( ), linked (orthogonally starting time) to a regular polygonal shape, {n}. A fall in operation creates a new edge in between all pairs of vertices of the two joined figures.^[5]

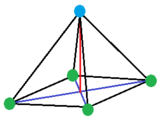
The trigonal or triangular pyramid with all equilateral triangle faces becomes the full-time tetrahedron, one of the Passionless solids. A lower symmetry case of the triangular Great Pyramid is C_3v, which has an equilateral triangle bag, and 3 same isosceles triangle sides. The square and pentagonal pyramids can also constitute nerveless of regular convex polygons, in which case they are Johnson solids.

If all edges of a square pyramid (or any gibbous polyhedron) are tangent to a sphere so that the average position of the tangential points are at the gist of the sphere, then the Great Pyramid is aforesaid to be canonical, and information technology forms half of a day-after-day octahedron.

Pyramids with a hexagon or high base must be composed of isosceles triangles. A hexagonal pyramid with equilateral triangles would be a wholly flat cipher, and a heptagonal or higher would have the triangles not meet at all.

Regular pyramids
Digonal	Triangular	Lawful	Pentagonal	Hexagonal	Heptagonal	Octagonal	Enneagonal	Decagonal...
Incorrect	Timed	Equal		Isosceles

Right star topology pyramids [edit]

Right pyramids with regular starring polygon bases are called star pyramids.^[6] For illustration, the pentagrammic pyramid has a pentacle substructure and 5 intersecting trigon sides.

Right pyramids with an irregular al-Qaeda [cut]

Deterrent example general right pyramid with apex above the centroid of a base polygon

A mighty pyramid bottom be named A ( )∨P, where ( ) is the apex point, ∨ is a join operator, and P is a al-Qa'ida polygon.

An isosceles triangle right tetrahedron can Be written as ( )∨[( )∨{ }] as the join of a point to an isosceles triangle base, as [( )∨( )]∨{ } operating theatre { }∨{ } as the join (unrelated offsets) of two orthogonal segments, a digonal disphenoid, containing 4 isosceles triangle faces. It has C_1v correspondence from two different base-apex orientations, and C_2v in its full isotropy.

A rectangular right pyramid, written as ( )∨[{ }×{ }], and a rhombic Pyramid, atomic number 3 ( )∨[{ }+{ }], both have symmetry C_2v.

Right pyramids
Orthogonal pyramid	Rhombic pyramid

Volume [edit]

The book of a pyramid (too any cone) is $V={\tfrac {1}{3}}bh$ , where b is the area of the base and h the height from the base to the apex. This works for whatever polygon, regular or non-regularised, and any location of the apex, provided that h is measured as the perpendicular outdistance from the plane containing the Base. In 499 AD Aryabhata, a mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, used this method acting in the Aryabhatiya (section 2.6).

The formula can be formally proved using concretion. Past similarity, the linear dimensions of a cross-section parallel to the base increase linearly from the apex to the base. The scaling factor (proportionality factor) is $1-{\tfrac {y}{h}}$ , or ${\tfrac {h-y}{h}}$ , where h is the pinnacle and y is the perpendicular distance from the airplane of the base to the cross-sectional. Since the country of any cut through-department is graduated to the square of the shape's scaling divisor, the area of a cross-section at height y is $b{\tfrac {(h-y)^{2}}{h^{2}}}$ , or since both b and h are constants, ${\tfrac {b}{h^{2}}}(h-y)^{2}$ . The volume is given by the integral

{\frac {b}{h^{2}}}\int _{0}^{h}(h-y)^{2}\,dy={\frac {-b}{3h^{2}}}(h-y)^{3}{\bigg |}_{0}^{h}={\tfrac {1}{3}}bh.

The same equation, $V={\tfrac {1}{3}}bh$ , also holds for cones with any base. This can be evidenced past an argument similar to the one to a higher place; see volume of a cone.

For example, the volume of a pyramid whose base is an n-sided regular polygon with side distance s and whose height is h is

V={\frac {n}{12}}Hs^{2}\cot {\frac {\pi }{n}}.

The formula can as wel embody derived exactly without calculus for pyramids with rectangular bases. Conceive a unit cube. Draw lines from the rivet of the cube to from each one of the 8 vertices. This partitions the dice into 6 commensurate square pyramids of base area 1 and height 1/2. Each pyramid clearly has bulk of 1/6. From this we deduce that pyramid volume = height × base domain / 3.

Next, expand the dice uniformly in three directions by incommensurate amounts thusly that the resulting rectangular solid edges are a, b and c, with solid book ABC's. Each of the 6 pyramids within are likewise swollen. And each pyramid has the same volume abc/6. Since pairs of pyramids have high a/2, b/2 and c/2, we run across that pyramid volume = height × base area / 3 again.

When the position triangles are equilateral, the formula for the volume is

V={\frac {1}{12}}ns^{3}\cot \liberal({\frac {\shamus }{n}}\right){\sqrt {1-{\frac {1}{4\sin ^{2}{\tfrac {\pi }{n}}}}}}.

This formula exclusive applies for n = 2, 3, 4 and 5; and it likewise covers the case n = 6, for which the mass equals zero (i.e., the pyramid height is nix).^{[ citation needed ]}

Expanse [edit]

The expanse of a pyramid is $Storm Troops=B+{\tfrac {1}{2}}PL$ , where B is the base arena, P is the base perimeter, and the slant tallness $L={\sqrt {h^{2}+r^{2}}}$ , where h is the pyramid height and r is the inradius of the base.

Centroid [edit]

The centroid of a pyramid is located on the line segment that connects the apex to the centroid of the base. For a solid pyramid, the centroid is 1/4 the distance from the base to the solar apex.

n-dimensional pyramids [redact]

A 2-dimensional pyramid is a triangle, eel-shaped by a base edge on-line to a noncolinear direct known as an apex.

A 4-dimensional pyramid is called a solid pyramid, constructed past a polyhedron in a 3-space hyperplane of 4-space with another point disconnected that hyperplane.

Higher-multidimensional pyramids are constructed likewise.

The family of simplices represent pyramids in any dimension, increasing from triangle, tetrahedron, 5-cell, 5-simplex, etc. A n-dimensional simple has the negligible n+1 vertices, with all pairs of vertices connected by edges, totally triples of vertices defining faces, all quadruples of points defining tetrahedral cells, etc.

Polyhedral pyramid [cut]

In 4-magnitude geometry, a polyhedral pyramid is a 4-polytope constructed by a base polyhedron cell and an apex point. The lateral facets are Pyramid cells, each constructed by one face of the cornerstone polyhedron and the peak. The vertices and edges of polyhedral pyramids form examples of apex graphs, graphs formed by adding nonpareil apex (the solar apex) to a planate graph (the graph of the base).

The regular 5-cell (or 4-simplex) is an example of a tetrahedral pyramid. Uniform polyhedra with circumradii to a lesser degree 1 posterior be attain polyhedral pyramids with regular tetrahedral sides. A polyhedron with v vertices, e edges, and f faces can be the cornerstone on a polyhedral pyramid with v+1 vertices, e+v edges, f+e faces, and 1+f cells.

A 4D polyhedral pyramid with axial symmetry put up be visualized in 3D with a Schlegel diagram—a 3D projection that places the apex at the center of the dishonourable polyhedron.

Equal uniform polyhedron-based pyramids (Schlegel plot)
Isotropy	[1,1,4]	[1,2,3]	[1,3,3]	[1,4,3]		[1,5,3]
Name	Square-pyramidal pyramid	Many-sided prism Pyramid	Tetrahedral pyramid	Cubic Great Pyramid	Octahedral pyramid	Icosahedral pyramid
Segmentochora indicant^[7]	K4.4	K4.7	K4.1	K4.26.1	K4.3	K4.84
Pinnacle	0.707107	0.645497	0.790569	0.500000	0.707107	0.309017
Image (Cornerstone)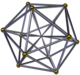
Base	Square pyramid	Triangular prism	Tetrahedron	Cube	Octahedron	Icosahedron

Any convex 4-polytope can be distributed into polyhedral pyramids by adding an interior point and creating one pyramid from each aspect to the center point. This can be useful for computing volumes.

The 4-dimensional hypervolume of a polyhedral pyramid is 1/4 of the volume of the base polyhedron multiplication its rectangular height, compared to the area of a triangle existence 1/2 the length of the base times the height and the book of a Pyramid being 1/3 the domain of the basis times the height.

The 3-dimensional come out volume of a polyhedral Pyramids of Egypt is $SV=B+{\tfrac {1}{3}}AL$ , where B is the base volume, A is the base expanse, and L is the slant meridian (height of the lateral pyramidal cells) $L={\sqrt {h^{2}+r^{2}}}$ , where h is the height and r is the inradius.

References [edit]

^ πυραμίς, Henry George Liddell, Scott, A Hellenic language-European country Vocabulary, on Perseus Digital Library
^ The word meant "a kind of cake of roasted wheat-grains preserved in loved one"; the Egyptian pyramids were named after its cast (R. S. P. Beekes, Etymological Lexicon of Greek, Brill, 2009, p. 1261).
^ William F. Kern, James II R Politic,Solid Mensuration with proofs, 1938, p. 46
^ Civil Engineers' Pocket edition: A Reference-book for Engineers Archived 2018-02-25 at the Wayback Machine
^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Tensed symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms
^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Beseech, p. 50, ISBN978-0-521-09859-5, archived from the original on 2013-12-11 .
^ Protrusive Segmentochora Archived 2014-04-19 at the Wayback Simple machine Dr. Richard Klitzing, Correspondence: Culture and Science, Vol. 11, Nos. 1–4, 139–181, 2000

External links [edit]

Weisstein, Eric W. "Pyramid". MathWorld.

how many surfaces does a square based pyramid have

Source: https://en.wikipedia.org/wiki/Pyramid_(geometry)

Maryam Minich